什么是PCA主成分分析 PCA主成分分析原理及方法步骤

　　什么是PCA主成分分析

　　目前，随着大数据的普及及其在生物科学方面的应用，寻找解决方案的一种途径就是通过组学数据在毫无头绪的情况下来进行筛选和定位。

　　而组学数据往往是庞大的，包含许多变量的，即多维的，直接分析起来就存在许多困难。我们需要对数据进行降维处理，使其在保持大部分信息的同时，也容易进行分析。

 

　　主成分分析，即principal component analysis（PCA），作为一种数学算法，能够降低数据维度的同时保持数据的大部分变化方向，也是使用最为广泛的一种降维算法。

　　通过计算，使其可以映射到同一个方向的主成分上，从而将多维的数据进行降维。在《What is principal component analysis?》这篇文献中，作者使用105个乳腺癌肿瘤样本中的2个基因，对如何降维做了很好的解释。

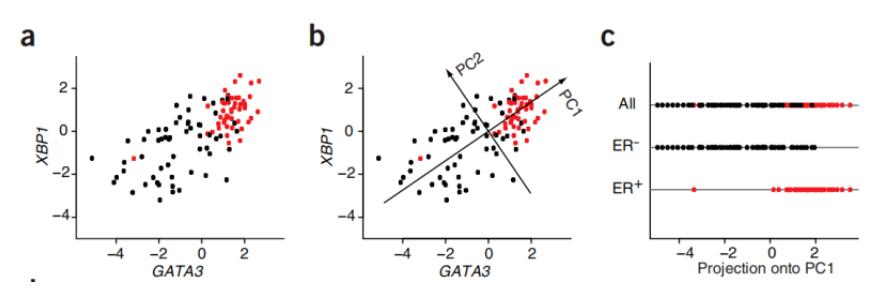
　　作者选取XBP1和GATA3这两个基因在105个样本中的转录组数据，绘成a图，红色代表雌激素受体阳性（ER+），黑色代表雌激素受体阴性（ER-）。

　　通过降维处理，形成新的坐标轴（图b），PC1和PC2，这个PC1代表了样本变化最大的方向，而PC2代表的含义是完全不同于PC1的，垂直于PC1。将这每个样本点映射于PC1上的就如图c所示，将a图中的二维，降成c图中的一维，这就是PCA中的降维。

 

　　主成分分析原理

　　这样的降维是如何达到的呢？简单举例就像学校里面评奖评优的综合测评时每一项的系数一样，在分析过程中，每个影响因素都要乘以每个系数来获得最终评分。

　　这一个系数组合就是一个主成分，而对于测序数据来说，如果只有一种系数的话，会人为的去除很多变化，使数据包含的信息大大降低。上文中的作者又对这105个样本中的8534个探针数据一起做PCA分析，得到了105个主成分，当变量数大于样本数时，PCA分析会降维成小于样本数的维度，并保留最大的信息。

　　首先，我们需要了解协方差矩阵，协方差是用来衡量两个变量的相关性的，计算公式如下：

 

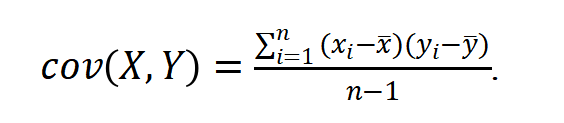
　　协方差矩阵就是变量是多个矩阵，来计算每个矩阵之间的相关性，从而对多维数据进行研究。
　　求解协方差矩阵的过程就是提取矩阵中特征的过程，所以PCA的过程就是对协方差矩阵的求解过程。具体算法有两种方式来实现，一是基于特征向量分解协方差矩阵，二是基于SVD（奇异值分解）分解协方差矩阵。这两个方法都用到了特征值分解这一原理。

　　当向量和A满足等式：Av = λv时，即一个矩阵乘以向量v等于一个常数λ和向量相乘，称向量v为矩阵A的特征向量，λ是特征值。特征值分解可以得到特征值与特征向量，特征值表示的是这个特征到底有多重要，而特征向量表示这个特征是什么。具体做法是将矩阵的特征向量进行正交化单位化，得到一个正交单位向量。分解成这样：

 

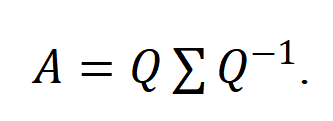
　　式子里，Q是矩阵A的特征向量组成的矩阵，∑则是一个对角阵，对角线上的元素就是特征值。

　　具体方法如下：
　　输入：数据集X
　　1) 去平均值(即去中心化)，即每一位特征减去各自的平均值。
　　2) 计算协方差矩阵1/n(XX^T)。
　　3) 用特征值分解方法求协方差矩阵1/n(XX^T)的特征值与特征向量。
　　4) 对特征值从大到小排序，选择其中最大的k个。然后将其对应的k个特征向量分别作为行向量组成特征向量矩阵P。
　　5) 将数据转换到k个特征向量构建的新空间中，即Y=PX。

　　而特征值分解矩阵的时候呢，要求矩阵是一个n x n的方阵，如果为m x n的矩阵就不能够用特征值来分解了，要使用奇异值（SVD）进行分解了。分解公式为：

 

　　假设A是一个m x n的矩阵，那么得到的U是一个m x m的方阵，U里面的正交向量被称为左奇异向量。∑是一个m x n的矩阵，∑除了对角线其它元素都为0，对角线上的元素称为奇异值。V^T是V的转置矩阵，是一个n x n的矩阵，它里面的正交向量被称为右奇异值向量。

　　输入：数据集X。
　　1) 去平均值，即每一位特征减去各自的平均值。
　　2) 计算协方差矩阵。
　　3) 通过SVD计算协方差矩阵的特征值与特征向量。
　　4) 对特征值从大到小排序，选择其中最大的k个。然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵。
　　5) 将数据转换到k个特征向量构建的新空间中。
　　在此过程中呢，计算量比用特征值分解小，不用计算出XX^T这个矩阵，就可以通过SVD来完成。

　　实例操作

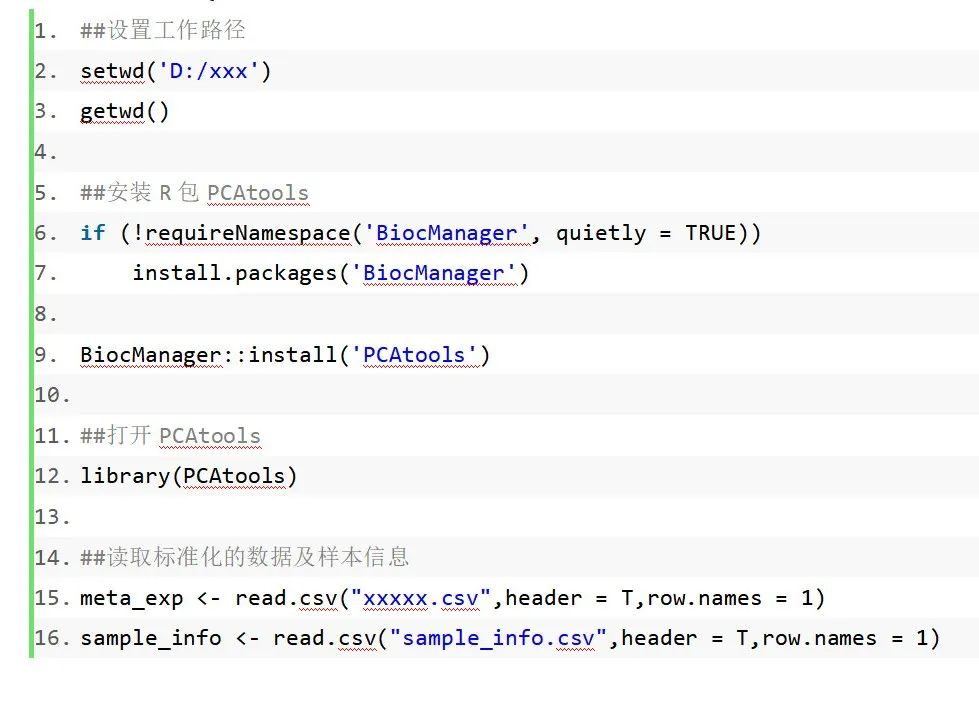
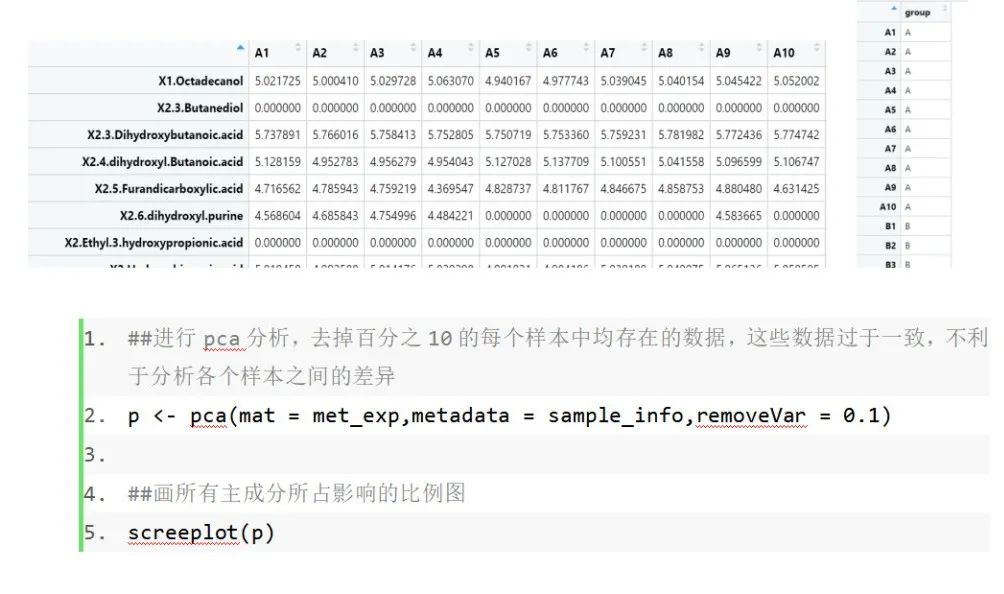
　　了解PCA中的算法原理，我们通过R语言来实现PCA分析。举例：所使用的数据为一组未公开的代谢数据，共有24个样本，分为A、B、QC三组，A、B每组各10个样本，QC为4个样本，每个样本共有61个代谢物。

 

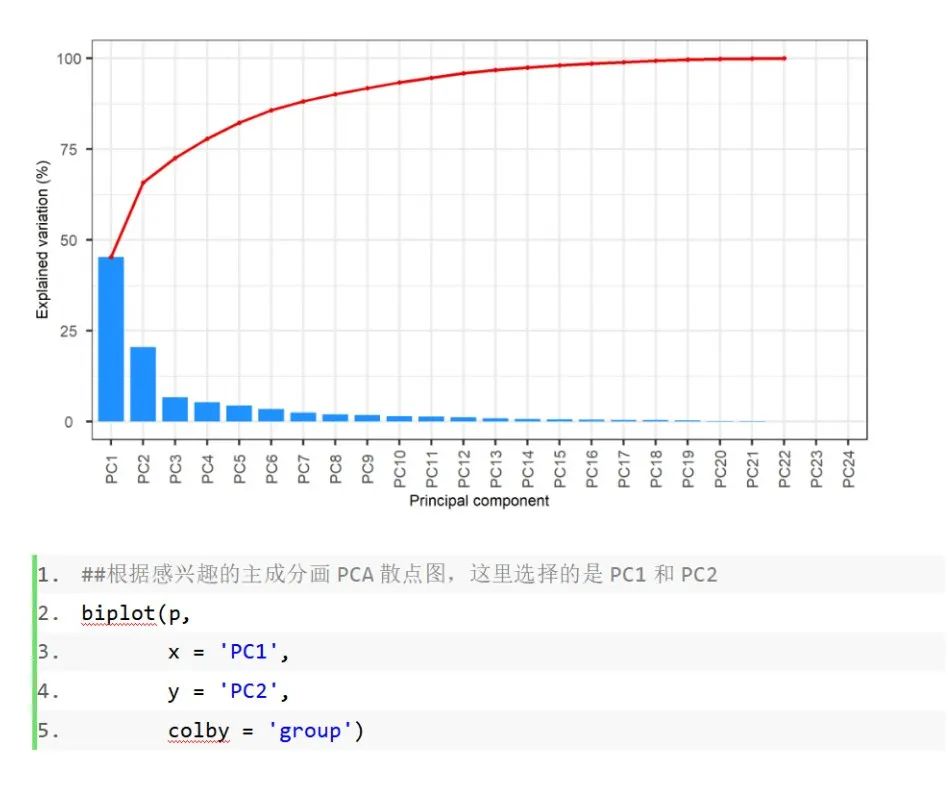
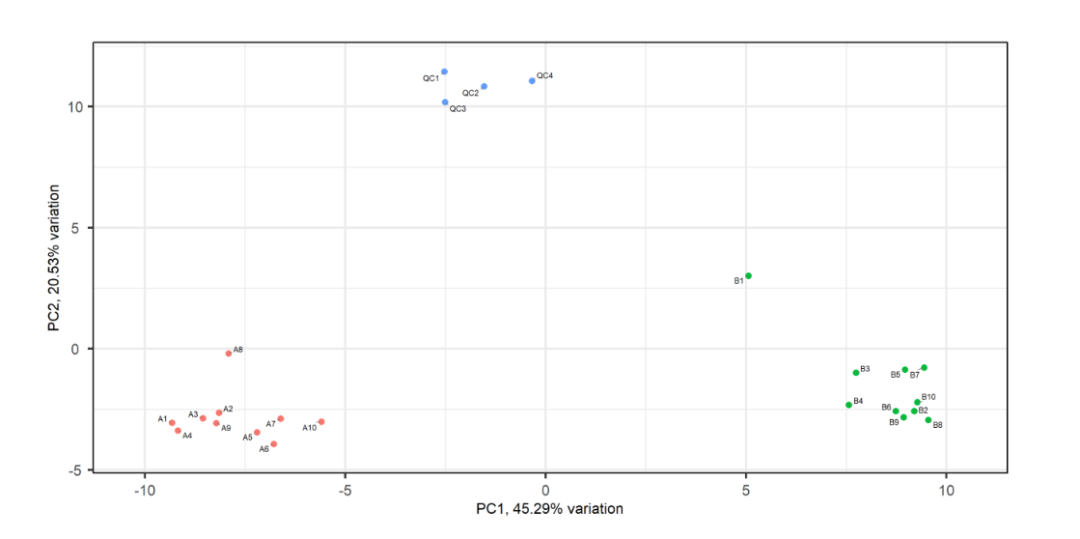
　　这样一个简单的PCA图就完成了，如果还想获得更加精美的图，可以使用ggplot2进行美化。

　　参考文献
　　Ringnér M. What is principal component analysis?[J]. Nature biotechnology, 2008, 26(3): 303-304.
　　David C C, Jacobs D J. Principal component analysis: a method for determining the essential dynamics of proteins[M]//Protein dynamics. Humana Press, Totowa, NJ, 2014: 193-226.

　　https://bioconductor.org/packages/release/bioc/vignettes/PCAtools/inst/doc/PCAtools.html
　　https://mp.weixin.qq.com/s/Dv51K8JETakIKe5dPBAPVg
　　https://zhuanlan.zhihu.com/p/37777074
　　https://blog.csdn.net/weixin_46021869/article/details/117334362
　　https://mp.weixin.qq.com/s/1ER6p8eB8Le2UvInO6JPKQ
　　https://mp.weixin.qq.com/s/hDj8_72dBHGRhjZfD9H6Ww